পর্যায়গত উপযোগ কি | উদাহরণ ও চিত্রসহ ব্যাখ্যা

 

পর্যায়গত উপযোগ (Ordinal utility)

উপযোগের পর্যায়গত পরিমাণ সম্পর্কে প্রাথমিক ধারণা দেন Pareto, Antonelli, Fisher প্রমুখ অর্থনীতিবিদ। পরবর্তী সময়ে Prof. J. R. Hicks এবং R. G. D Allen এ ব্যাপারে সুস্পষ্ট মতামত তুলে ধরেন। মার্শালের সংখ্যাগত উপযোগ ধারণাটির সমালোচনা করতে গিয়ে তাঁরা পর্যায়গত উপযোগ ধারণাটি প্রকাশ করেন। তাঁদের মতে, উপযোগকে কখনও সংখ্যা দ্বারা গণনা করা উচিত নয়, বরং উপযোগকে পর্যায়গতভাবে বা বিভিন্ন স্তরে বিভক্ত করে পরিমাপ করা উচিত। সুতরাং ভোক্তার উপযোগকে যখন সংখ্যাগতভাবে প্রকাশ না করে শুধু তুলনা করা হয়, তখন তাকে পর্যায়গত উপযোগ বলে। সাধারণত 1st, 2nd, 3rd ইত্যাদি হল পর্যায়গত (ordinal) সংখ্যা। আবার I, II, III ইত্যাদি রোমান সংখ্যাকেও পর্যায়গত সংখ্যা হিসেবে বিবেচনা করা যায়। এসব সংখ্যা পর্যায়গতভাবে সাজানো যায়। কিন্তু সাজানোর ধারা থেকে এসব সংখ্যার মধ্যকার পার্থক্য জানার কোন উপায় নেই। মনে করি এক লোক একটি কমলা থেকে আপেলের তুলনায় বেশি উপযোগ লাভ করে। এখন আমরা যদি কমলা হতে প্রাপ্ত উপযোগের জন্য 10 সংখ্যা ব্যবহার করি এবং আপেল হতে প্রাপ্ত উপযোগের জন্য 5 সংখ্যাটি ব্যবহার করি তাহলে পর্যায়গত উপযোগ পরিমাপের ক্ষেত্রে এ দু'টি সংখ্যার পার্থক্য কোন তাৎপর্য বহন করবে না। কেননা কমলার উপযোগ নির্দেশের জন্য 5 এর চেয়ে সংখ্যা বড় হলেই চলবে। সংখ্যাটি কত বড় হবে তার কোন তাৎপর্য পর্যায়গত পরিমাপের বেলায় নেই। উপযোগ পরিমাপের এ ধারণার ভিত্তিতে নিরপেক্ষ রেখা তত্ত্ব গড়ে উঠে। 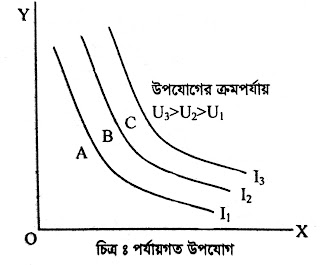নিরপেক্ষ রেখাগুলোকে পর্যায়ের ভিত্তিতে উপস্থাপন করা হলে, তাকে নিরপেক্ষ মানচিত্র বলে। বিষয়টি চিত্রের সাহায্যে নিম্নোক্তভাবে প্রকাশ করা যায়।